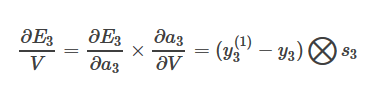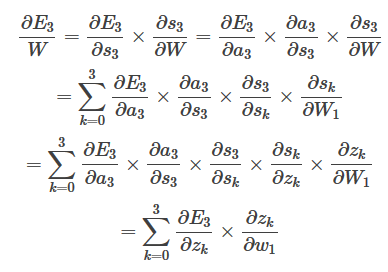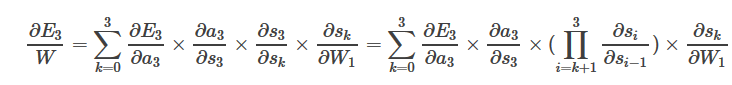RNN学习总结

RNN

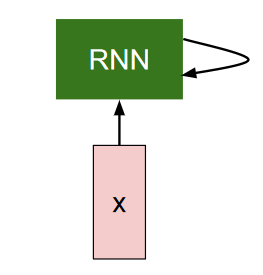
RNN，循环神经网络，是一种专门处理序列数据的神经网络，其基本结构如图所示：

simple_rnn

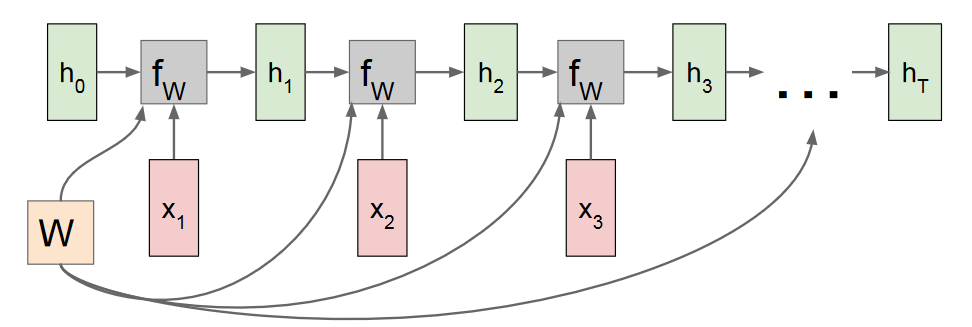
RNN的输入是序列数据x与上轮计算输出的隐藏状态。假设RNN的隐藏层计算为fw，隐藏状态为h，将其计算图展开，可以得到：

unfolding_rnn

值得注意是，每次隐藏层计算所需要的参数W，都是一样的，也就是所谓的共享参数。

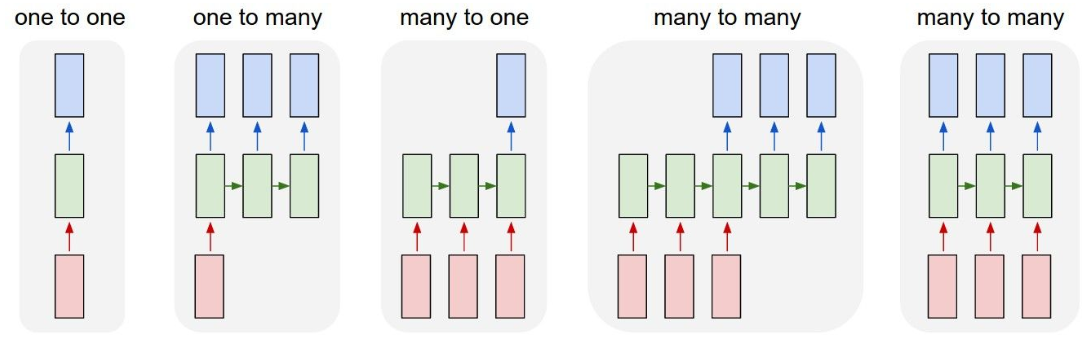
RNN根据输入输出是不是变长，可以分为下图中的右边四种。one-to-many比如是image captioning, many-to-one比如是sentiment classification, many-to-many比如是seq2seq，最后一种是video classification。

rnn

RNN的计算

拿一个简单的rnn拿做例子，讲讲rnn的前向与后向计算。

记隐藏状态为s，s = tanh(U*x + W * s)，a=f(a)， y=softmax(a)，loss为E，我们拿第三个time step举例。E对V的偏导数为：

bp1

其中对softmax的求导可参考这里。

E对W的偏导数较为复杂，因为求s3对W的偏导数时，而s3是s2的函数，s2也是W的函数。

bp2

值得注意的是，在这里，存在一个连乘

bp3

因而当序列过长时，必定造成梯度消失问题。而对于RNN时刻T的输出，是时刻t=1,…,T-1的输入综合作用的结果，也就是说更新模型参数时，要充分利用当前时刻以及之前所有时刻的输入信息。但是如果发生了梯度消失问题，就会意味着，距离当前时刻非常远的输入数据，不能为当前模型参数的更新做贡献，所以在RNN的编程实现中，才会有“truncated gradient”这一概念，只利用较近的时刻的序列信息，把那些“历史悠久的信息”忽略掉了。

RNN的后向计算，从图的角度来理解的话，看下图的红色线，需要经过多次W，即需要多次乘上W，非常容易导致梯度爆炸或梯度消失。

bp4

我们可以通过梯度裁剪（gradient clipping）解决梯度爆炸，而梯度消失问题，我们需要用到LSTM。

LSTM

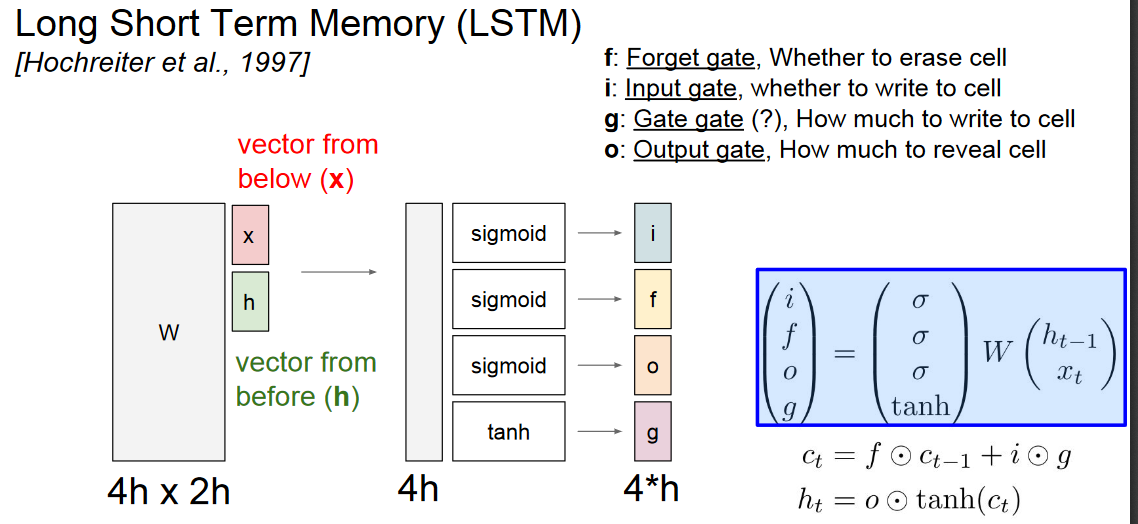
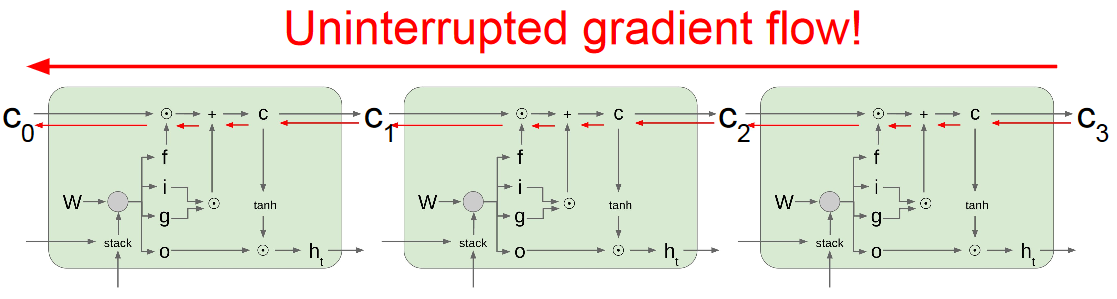
LSTM可由上图解释，通过4个门，来控制更新量。相比普通的rnn，在LSTM中，迭代的值有两个,ct和ht，f控制ct的遗忘程度，而i和g控制ct的更新程度，o则控制ct到ht的表达程度。上图其实已经是一个比较有总结性的图，由于i,f,o,g都需要一个wx,wh分别乘上x，h，即有4组wx,wh，那么就可以组成一个4*2的大矩阵W，一次性同时计算（TensorFlow的LSTM就是这么实现的）。

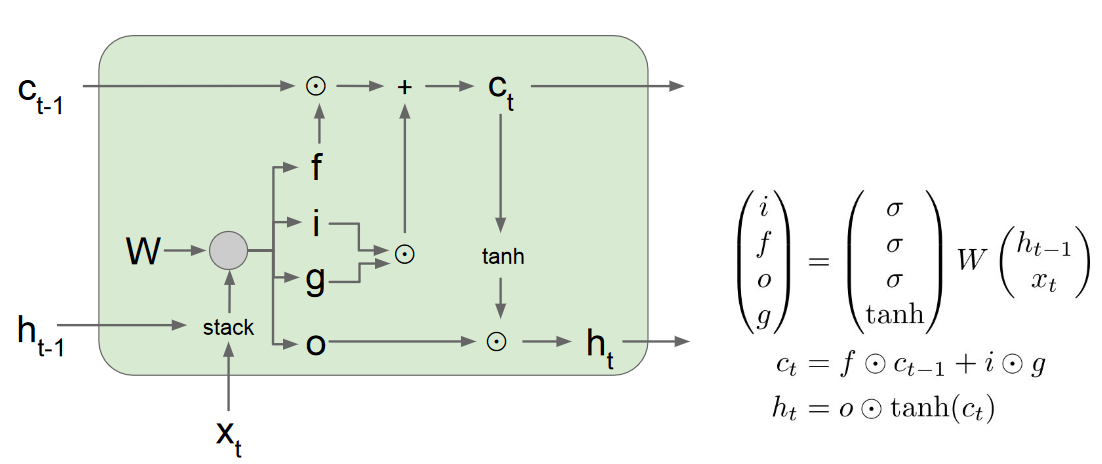
LSTM的图计算可以由下图表示:

LSTM2

那么为何LSTM能解决梯度消失问题呢？主要是由于：

相比普通RNN的在隐藏状态之间的求偏导需要矩阵相乘，在lstm中是大量的element-wise相乘
ct之间，存在一条梯度的高速通道，类似于resnet

Seq2Seq

seq2seq由encoder和decoder两部分组成，其中encoder部分可以看做是many-to-one，而decoder则是one-to-many。

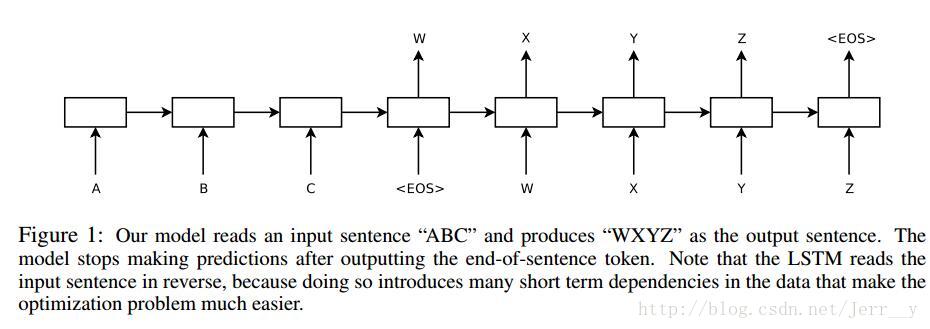
seq2seq

如图所示，将A,B,C通过rnn编码成W，W再通过rnn，解码成X,Y,Z。

Attention

从seq2seq角度来看，Attention是为了解决传统seq2seq长输入序列问题。

传统seq2seq会将输入序列不论长短，通过rnn编码成一个固定长度的状态向量(state vector)，这就导致，如果输入序列过长，那么这个向量难以保留全部的必要信息，导致后续解码时输入信息不足，模型性能差。

Attention机制其实很简单，既然只使用最后一个状态向量会造成信息损失，那么干脆把之前的状态向量都用好了，而attention机制起的作用就是选择恰当的状态向量。在大部分论文中，Attentions的实现是通过训练一个模型，输入是所有的encoder阶段的状态向量，输出是一个权重向量，代表各个输入的权重，权重越大，代表该输入越重要。更生动形象的图片可以参考这里。

额外的RNN代码

这是一个简单的RNN前向后向代码实例

def lossFun(inputs, targets, hprev):
  """
  inputs,targets are both list of integers.
  hprev is Hx1 array of initial hidden state
  returns the loss, gradients on model parameters, and last hidden state
  """
  xs, hs, ys, ps = {}, {}, {}, {}
  hs[-1] = np.copy(hprev)
  loss = 0
  # 前向计算
  for t in xrange(len(inputs)):
    # 对输入做one-hot encoding
    xs[t] = np.zeros((vocab_size,1)) 
    xs[t][inputs[t]] = 1
    # 计算隐藏层
    hs[t] = np.tanh(np.dot(Wxh, xs[t]) + np.dot(Whh, hs[t-1]) + bh) 
    # 计算输出层
    ys[t] = np.dot(Why, hs[t]) + by 
    # softmax
    ps[t] = np.exp(ys[t]) / np.sum(np.exp(ys[t])) 
    # cross-entropy loss，把真实目标的预测值拿出来求-log
    loss += -np.log(ps[t][targets[t],0]) 
  # 后向计算
  dWxh, dWhh, dWhy = np.zeros_like(Wxh), np.zeros_like(Whh), np.zeros_like(Why)
  dbh, dby = np.zeros_like(bh), np.zeros_like(by)
  dhnext = np.zeros_like(hs[0])
  for t in reversed(xrange(len(inputs))):
    # 这里是softmax求导，p-y
    dy = np.copy(ps[t])
    dy[targets[t]] -= 1 
    dWhy += np.dot(dy, hs[t].T)
    dby += dy
    dh = np.dot(Why.T, dy) + dhnext # backprop into h
    dhraw = (1 - hs[t] * hs[t]) * dh # backprop through tanh nonlinearity
    dbh += dhraw
    dWxh += np.dot(dhraw, xs[t].T)
    dWhh += np.dot(dhraw, hs[t-1].T)
    dhnext = np.dot(Whh.T, dhraw)
  for dparam in [dWxh, dWhh, dWhy, dbh, dby]:
    np.clip(dparam, -5, 5, out=dparam) # clip to mitigate exploding gradients
  return loss, dWxh, dWhh, dWhy, dbh, dby, hs[len(inputs)-1]

[cs231n](cs231n.stanford.edu/slides/2017/cs231n_2017_lecture10.pdf)

参考

RNN学习总结

RNN

RNN的计算

LSTM

Seq2Seq

Attention

额外的RNN代码

CATALOG

FEATURED TAGS

FRIENDS